2020-12-25

Making a Scene

raytracer rust

Chapter 7

The Ray Tracer Challenge: A Test-Driven Guide to Your First 3D Renderer (Pragmatic Bookshelf)

作者:Buck, Jamis
発売日: 2019/03/12
メディア: ペーパーバック

とりあえず object(球体)をそれっぽくレンダリングすることはできるようになった。とはいえ、このままでは object の数が増えると全ての object に対して個別に処理を行わなければならず、面倒くさい。
なので全ての object (と light) を管理する World を用意し、その World に対して Ray をどばすようにする。

"Making a Scene" というタイトルだから World じゃなくて Scene でも良い気もするけど。

Building a World

前述のように World は object と light を集約して管理するためのものなのでメンバもそれになる。

pub struct World {
    /// ライト
    lights: Vec<Light>,
    /// オブジェクト
    shapes: Vec<Sphere>,
}

あとは Ray との交差判定を行う intersect() で shapes に対してループする。

    pub fn intersect(&self, ray: &Ray) -> Vec<Intersection> {
        let mut intersections = vec![];
        for shape in &self.shapes {
            let mut xs = shape.intersect(ray);
            intersections.append(&mut xs);
        }

        intersections.sort_unstable_by(|i1, i2| {
            if i1.t < i2.t {
                std::cmp::Ordering::Less
            } else {
                std::cmp::Ordering::Greater
            }
        });

        intersections
    }

で、ここで得られた intersections の中で最も手前にある物がカメラから見える object になる。

この object に対して shading 等の計算をしていくわけだけれど、そこ用いる情報を必要になる度に計算していたのでは効率が悪いということで、事前にまとめて計算しておく。
本の中では computation という名前にしているが、これだと何を表しているのかが全くわからないということで、ここでは IntersectionState にした。これもあまり良い名前とは思えないから、良い名前を思いついたら変更予定。

pub struct IntersectionState<'a> {
    /// Ray と object が交差する場所での t
    pub(crate) t: f32,
    /// Ray と交差した object
    pub(crate) object: &'a Sphere,
    /// ワールド座標系における交差位置
    pub(crate) point: Point3D,
    /// ワールド座標系における視線ベクトル
    pub(crate) eyev: Vector3D,
    /// ワールド座標系における法線ベクトル
    pub(crate) normalv: Vector3D,
    /// Ray の起点が object 内部であるか
    pub(crate) inside: bool,
}

Defining a View Transformation

特に書くことはない。

Camera

今までは main() の中で行っていた Ray の生成処理を Camera にまとめる。この時、内部処理を出力画像のサイズから独立させるため、ray_for_pixel() ではカメラから 1 離れた位置にある平面を用いて Ray の生成を行っている。
この時、撮影する領域を表す平面は field_of_view と出力画像のアスペクト比から決定する。

結果

最終的に以下の画像が得られた。本の内容通りだと 100 x 50 で小さすぎるため、少し大きくしてある。

f:id:mtXTJocj:20201221094101p:plain

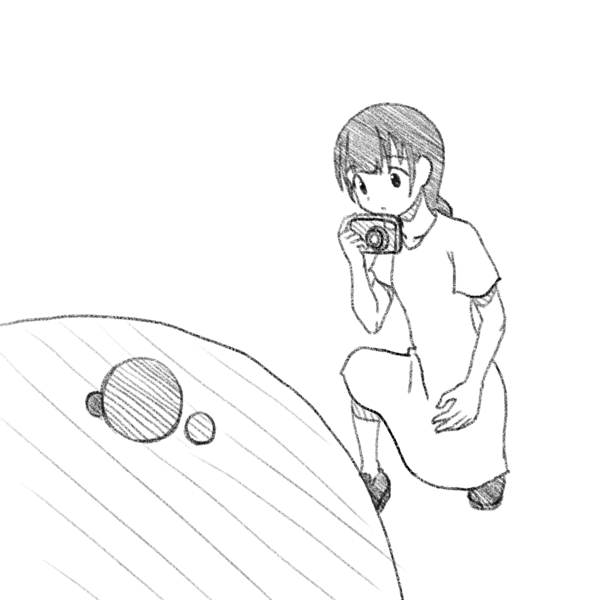
f:id:mtXTJocj:20201221092414p:plain

2020-12-22

Light and Shading

raytracer rust

Chapter 6

The Ray Tracer Challenge: A Test-Driven Guide to Your First 3D Renderer (Pragmatic Bookshelf)

作者:Buck, Jamis
発売日: 2019/03/12
メディア: ペーパーバック

前章まででとりあえず描画までは行くことができたものの、得られた画像は立体感がまったくなく平面的なものだった。
この章では Light を導入し、Shading 処理を加えることで影による立体感を出す。

この本で用いる Shading のモデルは非常にシンプルなもので、object(今のところ球のみ) 上の点(実際には微小平面)における shading の計算に要する情報は以下の通り。

光源位置
normal vector (法線ベクトル)
視点位置

Surface Normals

object(球)の normal vector は簡単に求められるが、それはあくまで球のローカル座標におけるものであり、他の座標系(ここではワールド)における normal vector を求めなくてはならない。その際、変換行列に non-uniform な scaling が含まれていたりすると変換行列をそのままかけただけでは変換後 object 上の normal vector にならない。
代わりに $(\mathbf{M}^{-1}) ^T$ を使う。

この本、test first で ray tracer を作っていくというもので、これだけだとボトムアップに ray tracer のことが理解できるように思えるのだけれど、実際には結構違う。複雑な部分のアルゴリズムは天下り式に与えられ、なぜそれでうまくいくのかの解説が全くないことがままある。
原理に興味がなくて、モノが作れればそれで ok という考え方なら問題ないけれど、プログラミングを通して理解を深めることを目的とするなら、ちょっと物足りない。

normal vector への Transform の適用もそれで、通常の変換行列 $\mathbf{M}$ の inverse transpose ( $(\mathbf{M}^{-1}) ^T$ ) を用いれば良いとだけ書かれている。

object 上の任意の点における normal vector を $\mathbf{n}$ 、tangent vector(接ベクトル)を $\mathbf{t}$ とする。両者は直交するため、

$\mathbf{n}\cdot\mathbf{t} = \mathbf{n}^T\mathbf{t} = 0$

が成り立つ( $T$ は transpose)。一方で Transform 適用後の $\mathbf{n}'$ 、 $\mathbf{t}'$ に対しても同様の関係が成り立つはずなので、

$\mathbf{n}'\cdot\mathbf{t}' = \mathbf{n}'^T\mathbf{t}' = 0$

となる。

ここで、Transform を $\mathbf{M}$ 、normal vector に適用する Transform を $\mathbf{S}$ とする。tangent vector は $\mathbf{M}$ をかけるだけで変換後の点で objct に接する性質は変わらないため

$\eqalign{ \mathbf{t}' &= \mathbf{M}\mathbf{t}\cr \mathbf{n}' &= \mathbf{S}\mathbf{n} }$

であり、両者が直交することから、

$\eqalign{ \mathbf{n}'\cdot\mathbf{t}' &= \mathbf{S}\mathbf{n}\cdot\mathbf{M}\mathbf{t} \cr &= (\mathbf{S}\mathbf{n})^T\mathbf{M}\mathbf{t}\cr &= \mathbf{n}^T\mathbf{S}^T\mathbf{M}\mathbf{t} = 0 }$

となる。 $\mathbf{n}^T\mathbf{t} = 0$ より $\mathbf{S}^T\mathbf{M} = \mathbf{I}$ ( $\mathbf{I}$ は単位行列)が成り立つことから、

$\eqalign{ \mathbf{S}^T &= \mathbf{M}^{-1}\cr \mathbf{S} &= (\mathbf{M}^{-1})^T }$

というわけで、 $(\mathbf{M}^{-1}) ^T$ を変換前の normal vector にかければ、変換後の objcet に対する normal vector が得られる。

The Phong Reflection Model

このモデルでは、Ambient、Diffuse、Specular の 3 要素に分け、それぞれを別々に計算してから合計する。合計する際の各要素の割合は Material に記述する。
それぞれの意味や計算手法は本に書かれているので、ここでは簡単に触れるにとどめる。

Ambient

環境光。定数値。

Diffuse

拡散反射光。object 上の微小平面と光源から発する光のなす角で決まる。微小平面の向きは normal vector で表されるため、normal vector と光源ベクトルから計算する。
使用する情報は

光源位置
normal vector (法線ベクトル)

Specular

鏡面反射光。Diffuse までは視点位置に無関係で、object 上の一点の色はどこから見ても同じになるが、これは視線も考慮に入れるためどこから見るかで変化する。
使用する情報は

光源位置
normal vector (法線ベクトル)
視点位置

Rendering

他は大体本に書かれている通りなので、この章の範囲まで実装した状態での rendering 結果を載せておく。

f:id:mtXTJocj:20201216164426p:plain

少しそれらしくなってきた。

f:id:mtXTJocj:20201220000441p:plain

2020-12-20

Linuxで動かしながら学ぶTCP/IPネットワーク

book network linux

1 台の Linux マシン上でネットワークを使って少し遊ぼうとしたとき、何を使えば良いのか調べたところ、Network Namespace が手ごろっぽい。とはいえ、一度も触ったことがなかったので以下の本を読んでみた。

Linuxで動かしながら学ぶTCP/IPネットワーク入門

作者:もみじあめ
発売日: 2020/02/29
メディア: Kindle版

なお、未読者に向けての内容紹介を書くつもりはない。

Network Namespace

本の中で Network Namespace を扱っているのは主に Chapter 3,4 にあたる。ここで、一台の Linux マシン上でネットワークを構築して色々と実験をする。具体的には 1 対 1 の通信から始まり、(静的ルーティングによる)ルータを介して異なるセグメント間での通信など、少しずつステップアップしていく。後の章に比べて丁寧な作りになっているのは良いのだけれど、ひたすら同じようなコマンドを何度も入力させられるのには閉口してしまい、構成を記述した JSON を読み込んでコマントを発行する Python スクリプトを書いてしまった。

書き捨て気味で他の人が使うようには書いていないけれど、一応掲載しておく。いちいちリポジトリを作るのも面倒なので長くなるけど gist で。

gist056f52f93e94aba7f87dd842eac9f6f9

各 Chapter に対応した JSON もアップしておいた。chapter3_1.json を使うなら

> python netns.py chapter3_1.json start

で開始。

> python netns.py chapter3_1.json stop

で終了。ちなみに python のバージョンは以下の通り。

> python --version
Python 3.7.3

前述のように他人が使うことは一切考慮していないため、エラーチェック等は全くしていない。

どーでもいーけど、JSON を手書きすると trailing comma でミスしやすいネ。

IPTables による Bridge 経由パケットのフィルタリング

chapter 4.5 では複数のホストをネットワークで繋ぐため、ブリッジを導入するのだけれど、自分の環境では ping が通らなかった。

理由は sysctl の net.bridge.bridge-nf-call-iptables が 1 になっていたためで、その場合は iptables によるフィルタリングが効いてしまう。とりあえず 0 にして無効化したところ ping が通るようになった。

なお、本書を読むにあたってこれの対応が一番難しかった。

f:id:mtXTJocj:20201219235744p:plain

その他の部分について

Chapter 5 以降はトランスポート層から上のレイヤを扱っている。内容は本当に表面をなぞるだけ。localhost 上で疎通確認して、それを tcpdump で覗いて終わり程度。今まで色々やってきた Network Namespace は DHCP や NAT といった複数ホストが必要になるときにちょっと使うだけ。ちなみに DHCP のコマンドを何も考えずにそのまま使ったら /etc/resolv.conf を書き変えられてしまって、後で名前解決ができなくなっているのに気付いた。

Chapter 8 では python によるソケットプログラミングを扱っているが、これもネットワークプログラミングの本なら一番最初の章で出てくるようなもの。全くの素人以外は読む必要はない。

というわけで Chapter 5 以降は Not for me だった。

おそらく本の作者もまともな解説をするつもりはなく、わかった気にさせることを目的としていると思う。こうした場合、より深く知りたい人向けに次のステップとなる書籍ガイドを付けるべきだけれど、そういったものはなし。参考文献は RFC と python 関連のネット上のドキュメントで、つまりは純粋に執筆に使用した文書のリストであってこの本の対象読者に役立ててもらうためのものではない。

余談

ネットワークについて全く知らない人向けに解説するとき、下のレイヤから説明するのと上から説明するのとではどちらが分かりやすいんでしょうかね。

2020-11-14

Intersecting Rays with Spheres

raytracer rust

Chapter5

The Ray Tracer Challenge: A Test-Driven Guide to Your First 3D Renderer (Pragmatic Bookshelf)

作者:Buck, Jamis
発売日: 2019/03/12
メディア: ペーパーバック

github.com

Ray

始点と方向のみ。

pub struct Ray {
    origin: Point3D,
    direction: Vector3D,
}

始点が同じ Ray を何度も作成することが頻繁にあるから、direction はともかく origin は reference にした方が良かったかも。必要なら後で変える。

Ray 上の任意の点 $\vec{p}$ は媒介変数 $t$ を用いて $\vec{p} = t\vec{direction} + \vec{origin}$ で表される。以降簡便のため $\vec{direction}$ を $\vec{d}$ 、 $\vec{origin}$ を $\vec{o}$ として扱う。

Sphere

ローカル座標において常に原点中心で半径 1 の単位球であるとする。これだけだと色々な位置に様々な大きさの球を配置することができない。とはいえ、ワールド座標でそれができれば良いのであるから、ワールド座標上での球は Transform を用いて表現する。つまり、ローカル座標 -> ワールド座標の変換行列を Sphere に持たせる。その変換で位置や大きさを決める。

pub struct Sphere {
    /// 球に対して適用する変換
    transform: Transform,
}

Intersecting Rays with Spheres

Intersection の計算は球のローカル座標で行う。こうすることで、原点中心の単位球との Intersection のみを考えれば良くなる。その際、Ray を Sphere のローカル座標で表現するためにワールド -> ローカルの変換、つまり Sphere が持つ transform の inverse を適用する。

原点に位置する単位球は [tex: x² + y² + z² - 1 = 0] で表される。これに上記 Ray を代入すると

$p_x^2 + p_y^2 + p_z^2 -1 = \\ (t d_x + o_x)^2 + (t d_y + o_y)^2 + (t d_z + o_z)^2 - 1 = \\ \vec{d}^{2}t^2 + \vec{o}^2 + 2(d_{x}o_{x} + d_{y}o_{y} + d_{z}o_{z})t -1 = \\ \vec{d}^{2}t^2 + 2\vec{d}\cdot\vec{o}t + \vec{o}^2 - 1 = 0$

となり、 $a = \vec{d}^{2}$ 、 $b = 2\vec{d}\cdot\vec{o}$ および $c = \vec{o}^2 - 1$ とおけば [tex: ax² + bx + c = 0] という二次方程式になる。なので解の公式がそのまま使え、

        let r = self.transform.inv() * ray;
        let o = r.origin();
        let d = r.direction();
        let sphere_to_ray = o - &Point3D::ZERO;

        let a = d.dot(&d);
        let b = 2.0 * d.dot(&sphere_to_ray);
        let c = sphere_to_ray.dot(&sphere_to_ray) - 1.0;

        let discriminant = b * b - 4.0 * a * c;
        if discriminant < 0.0 {
            // no intersection
            return vec![];
        }

        let t1 = (-b - discriminant.sqrt()) / (2.0 * a);
        let t2 = (-b + discriminant.sqrt()) / (2.0 * a);

で Ray と Sphere の交点を求めることができる。なお、sphere_to_ray は球の中心から Ray の始点方向へのベクトルを表している。単位球の中心が原点にあるなら、これは常に $\vec{o}$ に等しい。

Rendering

今のところ Camera が存在していないため、Rendering の処理において簡易的な Camera を実現する。必要な情報は以下の通り。

出力する画像の大きさ(pixel 単位 $I_w * tex: I_h$ )
撮影する平面(ワールド座標における大きさ $w * h$ )
撮影する平面までの距離

またCamera はワールド座標 (0, 0, -5) 位置し、z 軸正方向を向いているとする。

目的とする画像を得るには各 pixel が何色であるかを知らなければならない。そのため、各 pixel に対応する Ray を生成する。

上記を図示したのが以下。

f:id:mtXTJocj:20201114210222p:plain

ここで $I_w$ と $w$ , $I_y$ と $y$ , が対応しているとわかる。よって、x 方向は 1 pixel あたりの大きさはワールド座標系において $w / I_w$ になり、同様に y 方向は $h / I_h$ になる。今回は出力画像サイズを縦横ともに 100 pixel とし、撮影する平面は縦横ともに 7.0 とした。

    let wall_size = 7.0;
    let canvas_pixels: usize = 100;
    let size_per_pixel = wall_size / canvas_pixels as f32;

よって pixel 単位でループする際に size_per_pixel ずつ変化させる

    for y in 0..canvas.height() {
        let world_y = half - (size_per_pixel * y as f32);

        for x in 0..canvas.width() {
            let world_x = -half + (size_per_pixel * x as f32);

これと撮影する平面までの距離を合わせればワールド座標系での 1 点が決まり、カメラ位置とその点を結ぶ線が求める Ray の方向になる。

            let mut direction = &position - &ray_origin;
            direction.normalize();

            let r = Ray::new(ray_origin.clone(), direction);

こうして各 pixel に対して生成した Ray と Sphere とで交差判定を行い、交差する場合(赤)としない場合(黒)とで異なる色を出力すると以下のような画像が得られる。

f:id:mtXTJocj:20201114202025p:plain

まだ全然 3D らしくないネ。

f:id:mtXTJocj:20200118114540p:plain

2020-01-17

Matrix Transformations

raytracer rust

Chapter4

The Ray Tracer Challenge: A Test-Driven Guide to Your First 3D Renderer (Pragmatic Bookshelf)

作者:Jamis Buck
出版社/メーカー: Pragmatic Bookshelf
発売日: 2019/03/08
メディア: ペーパーバック

github.com

Transform

Transform が備えるべき要件は以下の通り

逆変換を取得可能
Point3D, Vector3D および Transform に対して適用可能

これらを実現するためにはどのような実装が良いかを考える。

逆変換を取得可能

Transform の実装にあたっては、そのままだと Matrix4x4 を wrap した程度に思えるけれど、後々のことを考えると悩ましい点がある。その点とは逆行列の扱い。Matrix4x4 に inverse() を実装したのだからそれを使うだけに思えるが、毎回 inverse() を呼んで逆行列を計算するは極めて非効率だ。

そのため、Transform には通常の Matrix4x4 を表す mat の他に逆行列 inv も持たせる。

pub struct Transform {
    mat: Matrix4x4,
    inv: Matrix4x4,
}

メンバの mat と inv を勝手にいじられるとまずいので pub は付けない。

直接のアクセスを禁止したため、inv で逆行列を取得できるようにしておく。

    pub fn inv(&self) -> &Matrix4x4 {
        &self.inv
    }

また、Tranform 作成時には同時に逆変換も作成しておく必要がある。その際、 translation, scaling, rotation は inverse() を使わずにもっと簡単な方法で計算できる。

translation の場合は逆方向に同じだけ移動してやれば良いから、移動成分の符号を変える。

    pub fn translation(x: f32, y: f32, z: f32) -> Self {
        let mat = Matrix4x4::new([
            1.0, 0.0, 0.0, x,
            0.0, 1.0, 0.0, y,
            0.0, 0.0, 1.0, z,
            0.0, 0.0, 0.0, 1.0,
        ]);
        let inv = Matrix4x4::new([
            1.0, 0.0, 0.0, -x,
            0.0, 1.0, 0.0, -y,
            0.0, 0.0, 1.0, -z,
            0.0, 0.0, 0.0, 1.0,
        ]);
        Transform { mat, inv }
    }

scaling は s 倍に対して 1/s 倍で元にもどるから、

    pub fn scaling(x: f32, y: f32, z: f32) -> Self {
        assert!(x != 0.0);
        assert!(y != 0.0);
        assert!(z != 0.0);

        let mat = Matrix4x4::new([
            x, 0.0, 0.0, 0.0,
            0.0, y, 0.0, 0.0,
            0.0, 0.0, z, 0.0,
            0.0, 0.0, 0.0, 1.0,
        ]);
        let inv = Matrix4x4::new([
            1.0 / x, 0.0, 0.0, 0.0,
            0.0, 1.0 / y, 0.0, 0.0,
            0.0, 0.0, 1.0 / z, 0.0,
            0.0, 0.0, 0.0, 1.0,
        ]);
        Transform { mat, inv }
    }

のようにする。ここで 0 倍のスケーリングには逆行列が存在しない。公開 API ならちゃんとエラーを返すようにすべきだが、ここでは assert で済ませておく。

rotation を表す行列は直交行列なので transpose をとればそれが逆行列になる。以下は x 軸まわりの回転の場合。

    pub fn rotation_x(a: f32) -> Self {
        let mat = Matrix4x4::new([
            1.0,     0.0,      0.0, 0.0,
            0.0, a.cos(), -a.sin(), 0.0,
            0.0, a.sin(),  a.cos(), 0.0,
            0.0, 0.0, 0.0, 1.0,
        ]);
        let inv = mat.transpose();
        Transform { mat, inv }
    }

上記以外(現在のところ shearing のみ)に限り、逆行列の計算に inverse() を呼ぶ。

Vector3D, Point3D および Transform に対して適用可能

Transform の適用は * で行えるように、Vector3D、Point3D および Transform のそれぞれに対して Mul trait を実装する。Vector3D と Point3D に関しては単に行列をかけてやれば良いだけで特筆すべきことは何もない。一方で Transform 同士の場合には通常の変換 mat だけはなく逆変換を表す inv も考慮しなければならない。

2 つの行列 $A$ と $B$ の積 $AB$ の逆行列は $(AB)^{-1} = B^{-1}A^{-1}$ になる。よって

    fn mul(self, t: &Transform) -> Self::Output {
        Transform {
            mat: &self.mat * &t.mat,
            inv: &t.inv * &self.inv,
        }
    }

で $AB$ に相当する Transform が得られ、ここでも inverse() を使わずに済む。

ところで、Transform にわざわざ逆行列 inv を持たせているが、これを適用するには

t.inv() * &p;

のように逆行列を取得し、それを直接 Point3D なり Vector3D にかけてやる必要がある。しかもこれでは逆変換を Transform に対して適用することができない。

本来的には逆変換を表す Transform を作成する API を用意すべきなのだろうが、基本的に逆変換はローカルな使用にとどまり、複雑な操作が不要であることからより簡易な形である行列の直接利用で済ませることにした。

f:id:mtXTJocj:20191222174113p:plain

2019-11-26

Matrices

raytracer rust

Chapter3

The Ray Tracer Challenge: A Test-Driven Guide to Your First 3D Renderer (Pragmatic Bookshelf)

作者: Jamis Buck
出版社/メーカー: Pragmatic Bookshelf
発売日: 2019/03/08
メディア: ペーパーバック
この商品を含むブログを見る

Matrix4x4

3D グラフィクスで使う行列は主に 4x4 行列なので、汎用性のある作りにするのではなく、4x4 行列専用の構造体を用意する。

4x4 行列は内部的に 1 次元の配列で持つ。

pub struct Matrix4x4 {
    m: [f32; 16],
}

その場合、並びの順序には row-major と column-major の 2通りが考えられるが、今回は row-major でいくことにする。つまり、以下の順序で並んでいるとみなす。

$\begin{pmatrix} 0 & 1 & 2 & 3 \\\ 4 & 5 & 6 & 7 \\\ 8 & 9 & 10 & 11 \\\ 12 & 13 & 14 & 15 \end{pmatrix}$

よって、i 行 j 列にアクセスしたい場合には、配列の

$i * 4 + j$

番目の要素にアクセスする。

    pub fn at(&self, row: usize, column: usize) -> f32 {
        debug_assert!(row < 4 && column < 4);

        self.m[row * 4 + column]
    }

行列式

行列の実装は素直に行っていることもあり、とりたてて書くことはあまりない。複雑なことをやっているのは逆行列の計算くらいで、この計算には一旦行列式を求める必要がある。

4x4 の行列式を直接計算するのは複雑ということで、余因子展開を利用してよりサイズの小さい行列から計算している。実際のところ 3x3 行列なら行列式の計算もそこまで複雑ではないけれど、本の記述に倣って 3x3 行列に対しても 2x2 の行列式から求めるようにする。

その際、内部的に Matrix3x3 と Matrix2x2 を用意する。これは逆行列の計算にのみ利用するものであり、他から使われることはない。よって pub は不要。

f:id:mtXTJocj:20191117204404p:plain

余談

今回はじめてはてなブログで数式を書いたのだけれど、おそろしく使いにくかった。& が勝手に "amp;" にされてしまい、解決するのに結構時間を使ってしまった。

こういうどうでも良いことに時間を使わされると、徒労感がすごいよね。得るものも何もないし。

2019-11-11

Drawing on a Canvas

raytracer rust

Chapter2

The Ray Tracer Challenge: A Test-Driven Guide to Your First 3D Renderer (Pragmatic Bookshelf)

作者: Jamis Buck
出版社/メーカー: Pragmatic Bookshelf
発売日: 2019/03/08
メディア: ペーパーバック
この商品を含むブログを見る

github.com

Color

基本的には Point3D や Vector3D と変わらない。x, y, z の代わりに red, green, blue になっている。

pub struct Color {
    pub red: f32,
    pub green: f32,
    pub blue: f32,
}

また、Point3D や Vector3D と違い、Color 同士の演算しかないため、こちらの方が簡単かも。

Canvas

内部的には単純な Color の配列として実装する。

pub struct Canvas {
    width: usize,
    height: usize,
    colors: Vec<Color>,
}

これで width x height の Canvas を表現する。(x, y) の Color には width * y + x でアクセスする。また、Canvas の原点は左上。

PPM への出力

PPM は以前にも扱ったことがあるけれど、その時はバイナリ形式だった。

mtxtjocj.hatenablog.com

一方で今回はテキスト形式。また、Color は各成分が f32 であるため、出力時には [0.0, 1.0] を u8 の [0, 255] に変換しなくてはならない。

                let c = self.color_at(j, i);
                let r = (c.red * 255.0).round().min(255.0).max(0.0) as u8;
                let g = (c.green * 255.0).round().min(255.0).max(0.0) as u8;
                let b = (c.blue * 255.0).round().min(255.0).max(0.0) as u8;

そして、本では PPM の制限として 1 行 70 カラムまでというのを強調しており、わざわざ 70 カラムを越えないことを確認するテストケースまで用意していた。この点に関しては毎行 1 pixel にすれば気にせずに済むため、そのようにしている。
というか、一行が 70 カラムを越えない範囲でなるべく多くの情報を詰め込もうとした結果、行あたりの pixel 数が変わってしまったり、同じ pixel の red, green, blue の途中で改行したりといったことが起こり得る。それではせっかくテキストで出力しているのに、分かりにくくなってしまうのではなかろうか。

f:id:mtXTJocj:20191104012457p:plain